Armagetron Advanced: PDCylinder Class Reference

PDCylinder::PDCylinder	(	const pVec &	e0,
		const pVec &	e1,
		const float	radOut0,
		const float	radIn0 = `0.0f`
	)			`[inline]`

Definition at line 280 of file pDomain.h.

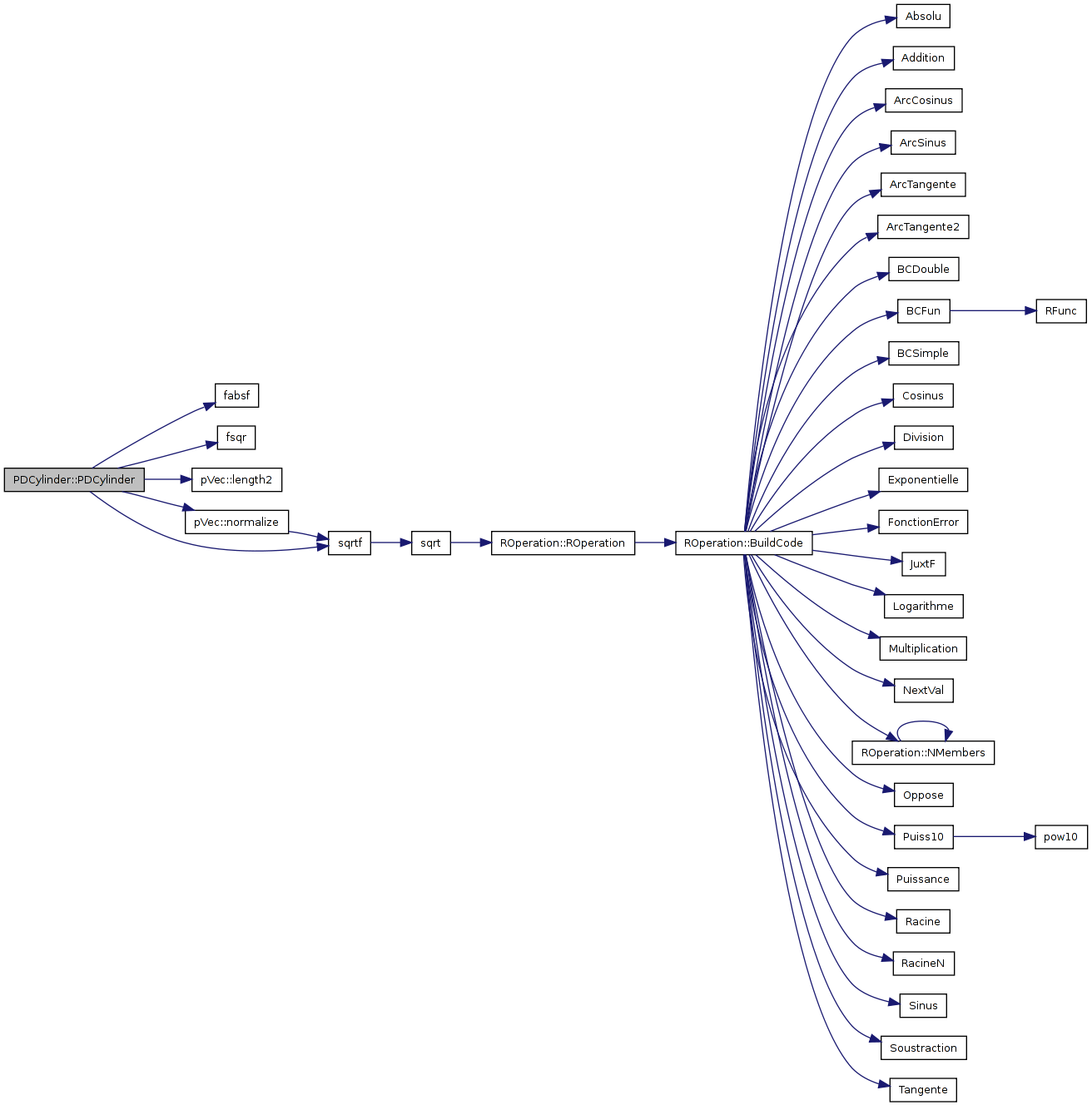
References apex, axis, axisLenInvSqr, fabsf(), fsqr(), pVec::length2(), pVec::normalize(), radDif, radIn, radInSqr, radOut, radOutSqr, sqrtf(), ThinShell, u, and v.

Referenced by copy().

00281     {
00282         apex = e0;
00283         axis = e1 - e0;
00284 
00285         if(radOut0 < radIn0) {
00286             radOut = radIn0; radIn = radOut0;
00287         } else {
00288             radOut = radOut0; radIn = radIn0;
00289         }
00290         radOutSqr = fsqr(radOut);
00291         radInSqr = fsqr(radIn);
00292 
00293         ThinShell = (radIn == radOut);
00294         radDif = radOut - radIn;
00295 
00296         // Given an arbitrary nonzero vector n, make two orthonormal
00297         // vectors u and v forming a frame [u,v,n.normalize()].
00298         pVec n = axis;
00299         float axisLenSqr = axis.length2();
00300         axisLenInvSqr = axisLenSqr ? (1.0f / axisLenSqr) : 0.0f;
00301         n *= sqrtf(axisLenInvSqr);
00302 
00303         // Find a vector orthogonal to n.
00304         pVec basis(1.0f, 0.0f, 0.0f);
00305         if (fabsf(basis * n) > 0.999f)
00306             basis = pVec(0.0f, 1.0f, 0.0f);
00307 
00308         // Project away N component, normalize and cross to get
00309         // second orthonormal vector.
00310         u = basis - n * (basis * n);
00311         u.normalize();
00312         v = Cross(n, u);
00313     }

Here is the call graph for this function:

Here is the caller graph for this function:

PDCylinder::~PDCylinder ( ) [inline]

Definition at line 315 of file pDomain.h.

00316     {
00317     }

bool PDCylinder::Within ( const pVec & pos ) const [inline, virtual]

Implements pDomain.

Definition at line 319 of file pDomain.h.

References apex, axis, axisLenInvSqr, pVec::length2(), radOutSqr, and x.

00320     {
00321         // This is painful and slow. Might be better to do quick accept/reject tests.
00322         // Axis is vector from base to tip of the cylinder.
00323         // x is vector from base to pos.
00324         //         x . axis
00325         // dist = ---------- = projected distance of x along the axis
00326         //        axis. axis   ranging from 0 (base) to 1 (tip)
00327         //
00328         // rad = x - dist * axis = projected vector of x along the base
00329 
00330         pVec x = pos - apex;
00331 
00332         // Check axial distance
00333         float dist = (axis * x) * axisLenInvSqr;
00334         if(dist < 0.0f || dist > 1.0f)
00335             return false;
00336 
00337         // Check radial distance
00338         pVec xrad = x - axis * dist; // Radial component of x
00339         float rSqr = xrad.length2();
00340 
00341         return (rSqr <= radInSqr && rSqr >= radOutSqr);
00342     }

Here is the call graph for this function:

pVec PDCylinder::Generate ( ) const [inline, virtual]

Implements pDomain.

Definition at line 344 of file pDomain.h.

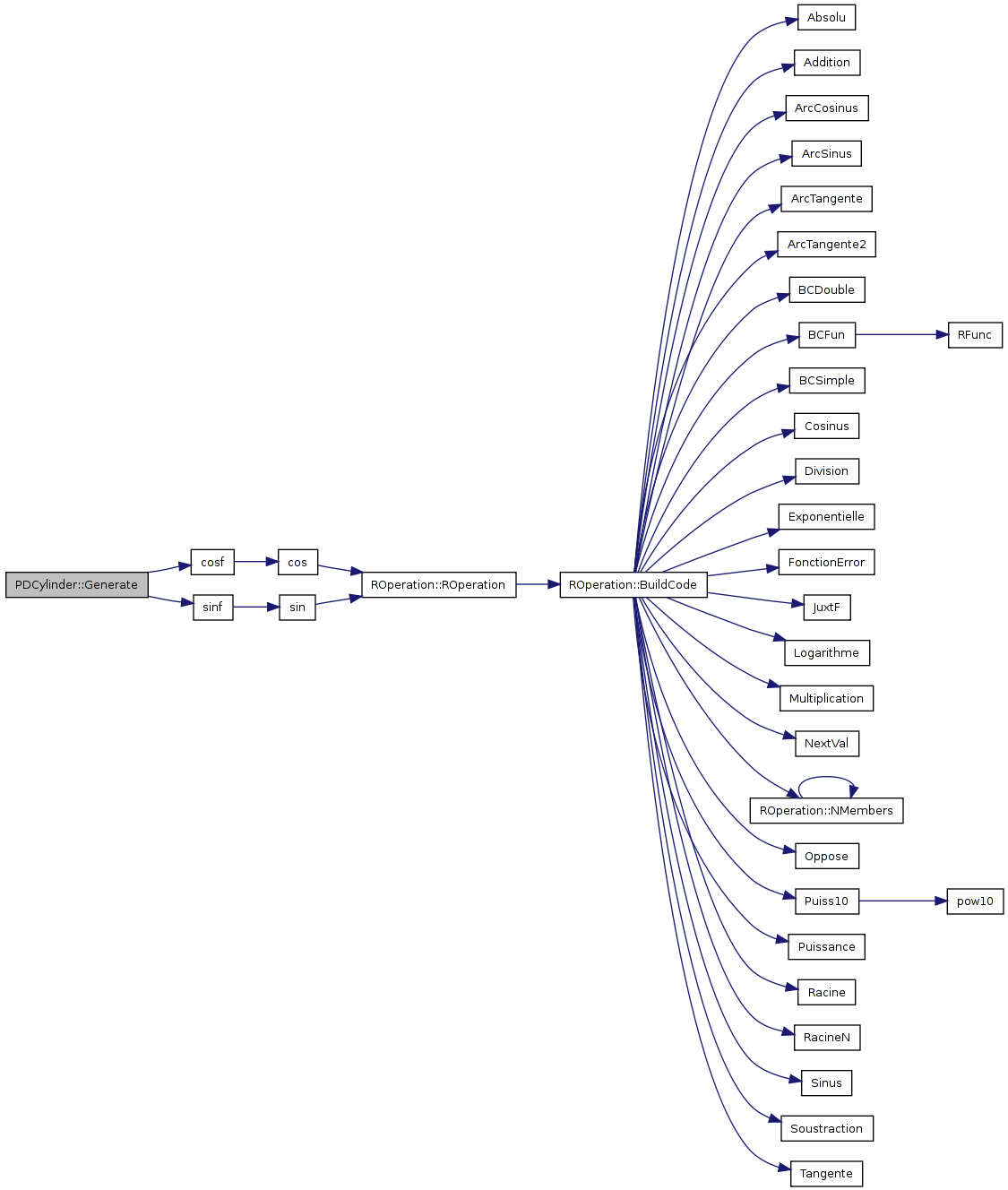
References apex, axis, cosf(), M_PI, pos, pRandf, radDif, radIn, sinf(), u, v, and x.

00345     {
00346         float dist = pRandf(); // Distance between base and tip
00347         float theta = pRandf() * 2.0f * float(M_PI); // Angle around axis
00348         // Distance from axis
00349         float r = radIn + pRandf() * radDif;
00350 
00351         // Another way to do this is to choose a random point in a square and keep it if it's in the circle.
00352         float x = r * cosf(theta);
00353         float y = r * sinf(theta);
00354 
00355         pVec pos = apex + axis * dist + u * x + v * y;
00356         return pos;
00357     }

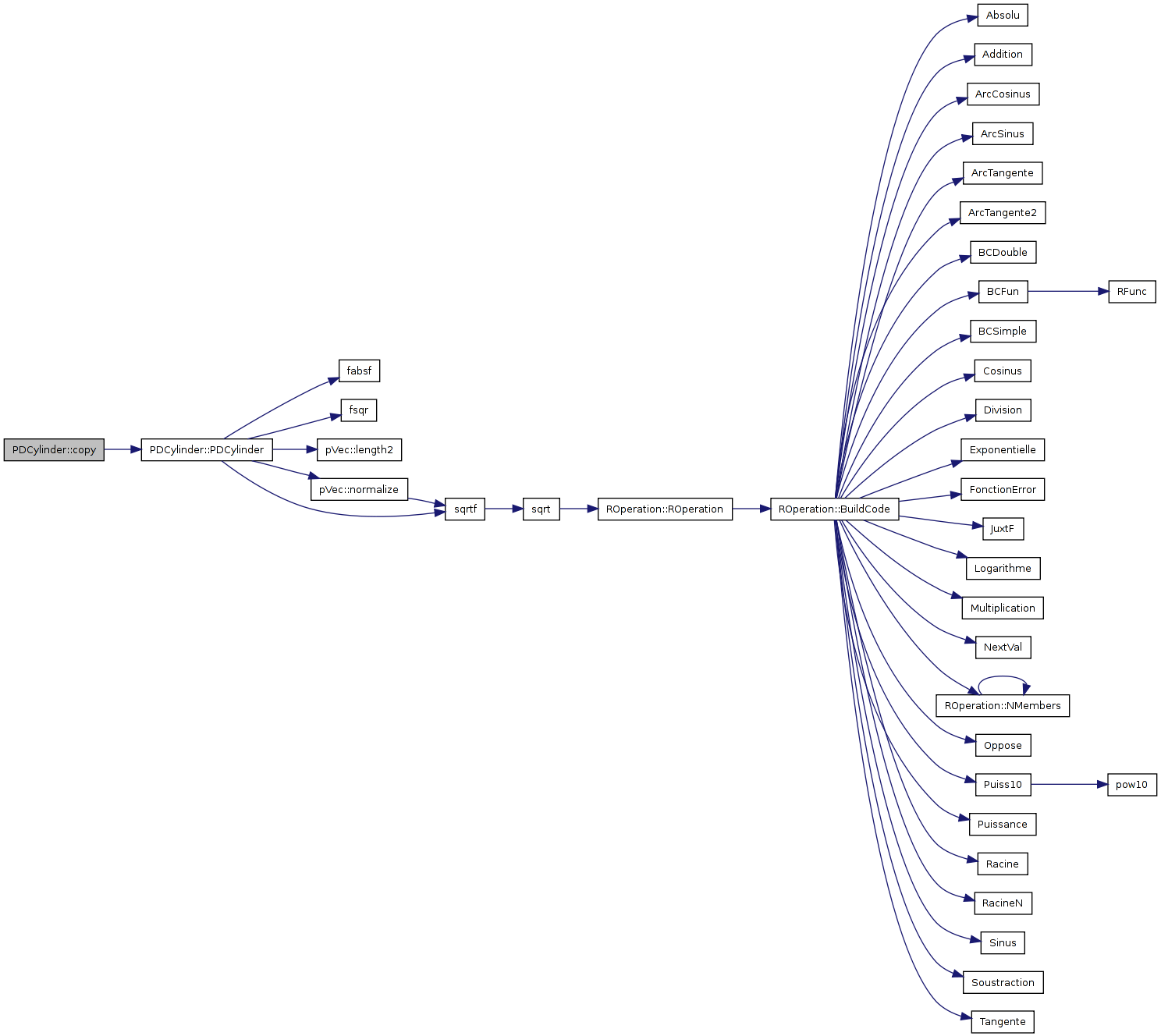
Here is the call graph for this function:

pDomain* PDCylinder::copy ( ) const [inline, virtual]

Implements pDomain.

Definition at line 359 of file pDomain.h.

References PDCylinder().

00360     {
00361         PDCylinder *P = new PDCylinder(*this);
00362         return P;
00363     }

Here is the call graph for this function:

pVec PDCylinder::apex

Definition at line 275 of file pDomain.h.

Referenced by Generate(), PDCylinder(), and Within().

pVec PDCylinder::axis

Definition at line 275 of file pDomain.h.

Referenced by Generate(), PDCylinder(), and Within().

pVec PDCylinder::u

Definition at line 275 of file pDomain.h.

Referenced by Generate(), and PDCylinder().

pVec PDCylinder::v

Definition at line 275 of file pDomain.h.

Referenced by Generate(), and PDCylinder().

float PDCylinder::len