tCoord Class Reference

Stores any kind of x and y coordinates. More...

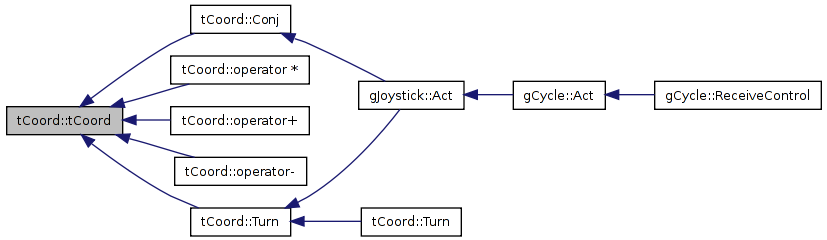
#include <tCoord.h>

List of all members.

Public Member Functions
	tCoord (REAL X=0, REAL Y=0)
bool	operator== (const tCoord &a) const
	Default constructor.
bool	operator!= (const tCoord &a) const
	Are the two coordinates far apart from each other to be considered different?
tCoord	operator- (const tCoord &a) const
	substracts two coordinates
tCoord	operator- () const
	mirrors a coordinate around the x and y axis
tCoord	operator+ (const tCoord &a) const
	adds two coordinates
const tCoord &	operator+= (tCoord const &other)
	adds two coordinates
const tCoord &	operator-= (tCoord const &other)
	substracts two coordinates
tCoord	operator * (REAL a) const
	stretches a coordinate by a factor from the center
const tCoord &	operator *= (REAL a)
	stretches a coordinate by a factor from the center
const tCoord &	operator *= (tCoord const &other)
	stretches a coordinate by a factor from the center
REAL	NormSquared () const
	returns the square of the distance to the origin
REAL	Norm () const
	returns the distance to the orign
void	Normalize ()
	normalizes the coordinate by setting the distance to the orign to 1 and keeping the ratio of the x and y coordinates
const tCoord &	operator= (const tCoord &a)
	overwrites a coordinate with another one
REAL	operator * (const tCoord &a) const
tCoord	Turn (const tCoord &a) const
	complex multiplication: turns this by angle given in a
tCoord	Turn (REAL x, REAL y) const
	complex multiplication: turns this by angle given in x and y
tCoord	Conj () const
	complex conjugation
void	Print (std::ostream &s) const
	Prints the coordinate into a stream (format: "(x,y)").
void	Read (std::istream &s)
	Reads the coordinate from a stream (format: "(x,y)").
Static Public Member Functions
static REAL	F (const tCoord &a, const tCoord &b)
	scalar product
static REAL	V (const tCoord &a, const tCoord &b, const tCoord &c)
static REAL	CrossProduct (tCoord const &a, tCoord const &b, tCoord const &c)
	returns the cross product of the three given points, whatever that is--code taken from http://en.wikipedia.org/wiki/Graham_scan
static REAL	Tangent (tCoord const &a, tCoord const &b)
	returns delta y over delta x
template<typename T>
static void	GrahamScan (T &in, T &out)
	finds the smallest convex polygon completely surrounding all points in in and stores them in out. See also http://en.wikipedia.org/wiki/Graham_scan
Public Attributes
REAL	x
REAL	y
	the stored coordinates
Classes
class	GrahamComparator

---

Detailed Description

Stores any kind of x and y coordinates.

Definition at line 40 of file tCoord.h.

---

Constructor & Destructor Documentation

tCoord::tCoord	(	REAL	X = 0,
		REAL	Y = 0
	)			[inline, explicit]

Definition at line 43 of file tCoord.h.

Referenced by Conj(), operator *(), operator+(), operator-(), and Turn().

:x(X),y(Y){}; 

Here is the caller graph for this function:

---

Member Function Documentation

bool tCoord::operator==

(

const tCoord &

a

)

const [inline]

Default constructor.

Are the two coordinates close enough to each other to be considered equeal?

Parameters:

a

the other coordinate

Returns:

are the coordinates close to each other to count as equeal?

Definition at line 136 of file tCoord.h.

References EPS, NormSquared(), and se_EstimatedRangeOfMult().

Referenced by operator!=().

                                                   {
    return ((*this-a).NormSquared()<=(EPS*EPS)*se_EstimatedRangeOfMult(*this,a));
}

Here is the call graph for this function:

Here is the caller graph for this function:

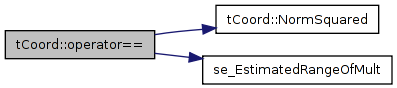
bool tCoord::operator!=

(

const tCoord &

a

)

const [inline]

Are the two coordinates far apart from each other to be considered different?

Definition at line 47 of file tCoord.h.

References operator==().

Here is the call graph for this function:

tCoord tCoord::operator-

(

const tCoord &

a

)

const [inline]

substracts two coordinates

Definition at line 48 of file tCoord.h.

References tCoord(), x, and y.

Here is the call graph for this function:

tCoord tCoord::operator-

(

)

const [inline]

mirrors a coordinate around the x and y axis

Definition at line 49 of file tCoord.h.

References tCoord(), x, and y.

Here is the call graph for this function:

tCoord tCoord::operator+

(

const tCoord &

a

)

const [inline]

adds two coordinates

Definition at line 50 of file tCoord.h.

References tCoord(), x, and y.

Here is the call graph for this function:

const tCoord& tCoord::operator+=

(

tCoord const &

other

)

[inline]

adds two coordinates

Definition at line 51 of file tCoord.h.

References x, and y.

const tCoord& tCoord::operator-=

(

tCoord const &

other

)

[inline]

substracts two coordinates

Definition at line 52 of file tCoord.h.

References x, and y.

tCoord tCoord::operator *

(

REAL

a

)

const [inline]

stretches a coordinate by a factor from the center

Definition at line 53 of file tCoord.h.

References tCoord(), x, and y.

Here is the call graph for this function:

const tCoord& tCoord::operator *=

(

REAL

a

)

[inline]

stretches a coordinate by a factor from the center

Definition at line 54 of file tCoord.h.

References x, and y.

const tCoord& tCoord::operator *=

(

tCoord const &

other

)

[inline]

stretches a coordinate by a factor from the center

Definition at line 55 of file tCoord.h.

References x, and y.

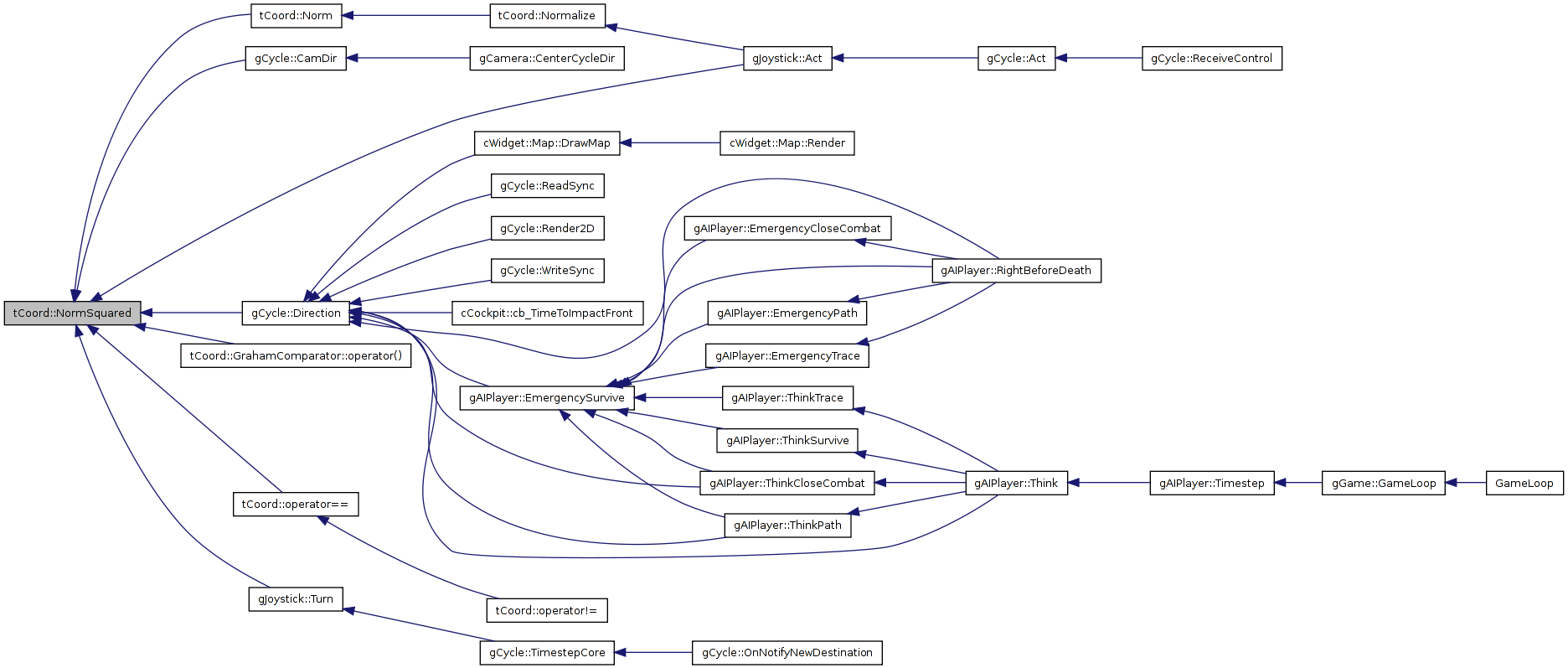
REAL tCoord::NormSquared

(

)

const [inline]

returns the square of the distance to the origin

Definition at line 56 of file tCoord.h.

References x, and y.

Referenced by gJoystick::Act(), gCycle::CamDir(), gCycle::Direction(), Norm(), tCoord::GrahamComparator::operator()(), operator==(), and gJoystick::Turn().

Here is the caller graph for this function:

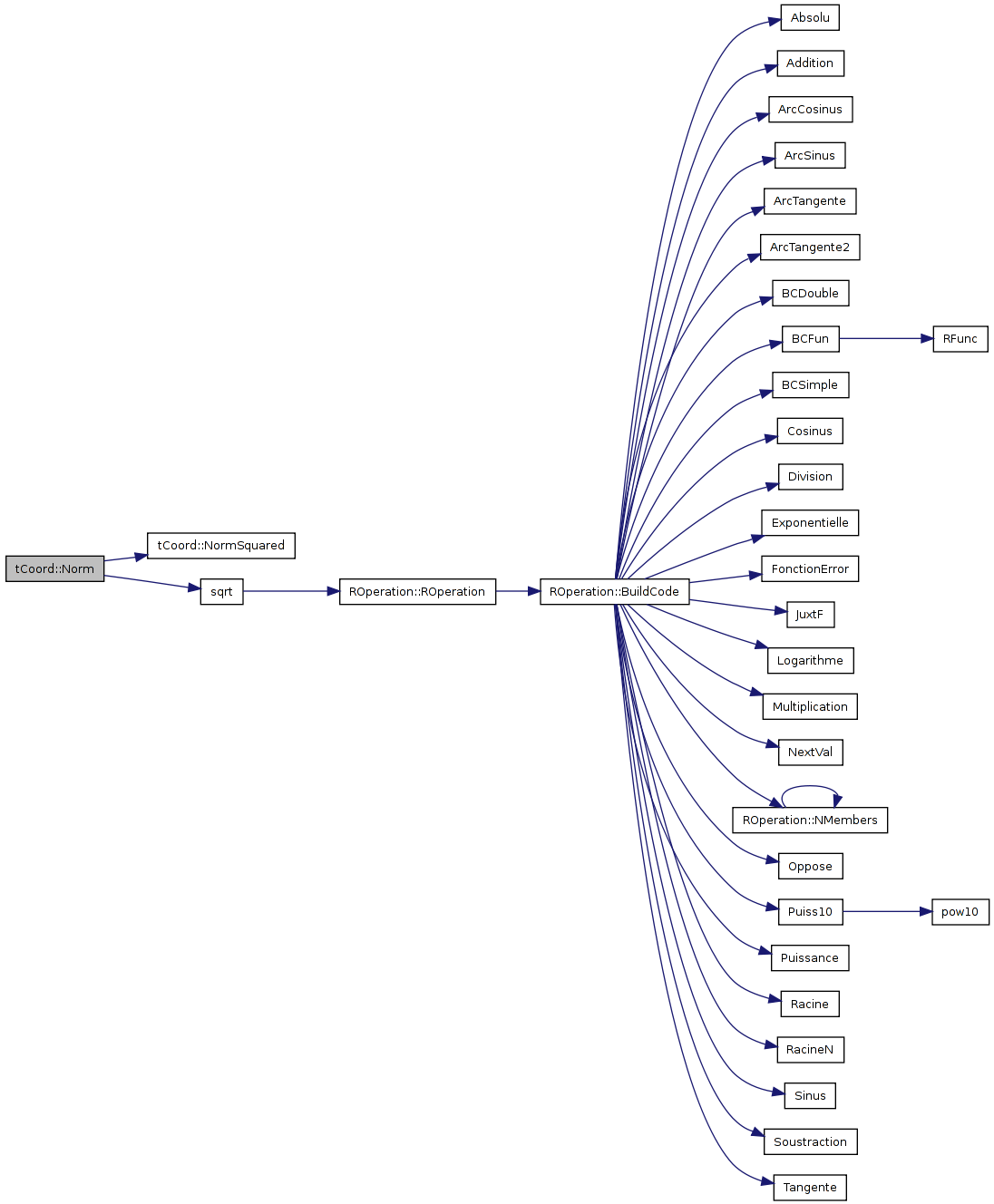
REAL tCoord::Norm

(

)

const [inline]

returns the distance to the orign

Definition at line 57 of file tCoord.h.

References NormSquared(), and sqrt().

Referenced by Normalize().

Here is the call graph for this function:

Here is the caller graph for this function:

void tCoord::Normalize

(

)

[inline]

normalizes the coordinate by setting the distance to the orign to 1 and keeping the ratio of the x and y coordinates

Definition at line 58 of file tCoord.h.

References Norm().

Referenced by gJoystick::Act().

Here is the call graph for this function:

Here is the caller graph for this function:

const tCoord& tCoord::operator=

(

const tCoord &

a

)

[inline]

overwrites a coordinate with another one

Definition at line 59 of file tCoord.h.

References x, and y.

static REAL tCoord::F	(	const tCoord &	a,
		const tCoord &	b
	)			[inline, static]

scalar product

Definition at line 62 of file tCoord.h.

References x, and y.

Referenced by V().

                                                  {
        return(a.x*b.x+a.y*b.y);
    }

Here is the caller graph for this function:

static REAL tCoord::V	(	const tCoord &	a,
		const tCoord &	b,
		const tCoord &	c
	)			[inline, static]

change coordinates, so that a is at zero and c is at one. gives the coordinate of b.

Definition at line 68 of file tCoord.h.

References ab, and F().

                                                                  {
        tCoord ab=b-a;
        tCoord ac=c-a;
        return(F(ab,ac)/F(ac,ac));
    }

Here is the call graph for this function:

static REAL tCoord::CrossProduct	(	tCoord const &	a,
		tCoord const &	b,
		tCoord const &	c
	)			[inline, static]

returns the cross product of the three given points, whatever that is--code taken from http://en.wikipedia.org/wiki/Graham_scan

Definition at line 75 of file tCoord.h.

References x, and y.

Referenced by GrahamScan().

                                                                                {
        return (b.x - a.x)*(c.y - a.y) - (c.x - a.x)*(b.y - a.y);
    }

Here is the caller graph for this function:

static REAL tCoord::Tangent	(	tCoord const &	a,
		tCoord const &	b
	)			[inline, static]

returns delta y over delta x

Definition at line 80 of file tCoord.h.

References x, and y.

Referenced by tCoord::GrahamComparator::operator()().

                                                          {
        return (b.y - a.y)/(b.x-a.x);
    }

Here is the caller graph for this function:

template<typename T>

void tCoord::GrahamScan	(	T &	in,
		T &	out
	)			[inline, static]

finds the smallest convex polygon completely surrounding all points in in and stores them in out. See also http://en.wikipedia.org/wiki/Graham_scan

Parameters:

	in	the standard container containing the tCoords to wrap into a rubber band. In will be modified!
	out	the standard container to put the rubber band into, its contents will be erased

Definition at line 163 of file tCoord.h.

References CrossProduct(), EPS, tASSERT, x, and y.

Referenced by eWallRim::UpdateBounds().

                                                          {
    tASSERT(!in.empty());
    out.clear();

    // find the point that's closest to the bottom, preferring points to the left
    tCoord P=in.front();
    typename T::iterator iter(in.begin()+1);
    for(; iter != in.end(); ++iter) {
        if(iter->y < P.y || iter->y == P.y && iter->x < P.x) {
            P = *iter;
        }
    }

    std::sort(in.begin(), in.end(), GrahamComparator(P));

    //std::cerr << "P: " << P << std::endl;

    out.push_back(P);
    for(typename T::iterator iter = in.begin()+1; iter != in.end(); ++iter) {
        if(*iter != P) {
            out.push_back(*iter);
            break;
        }
    }
    if(out.size()<2) return; //all points equeal P, kinda boring...

    //std::copy(in.begin(), in.end(), std::ostream_iterator<tCoord>(std::cerr, " "));
    //std::cerr << std::endl;
    for(typename T::iterator iter = in.begin(); iter != in.end(); ++iter) {
        //std::cerr << "New point: " << *iter << "; angle=" << (atanf(Tangent(P, *iter))*180/M_PI) << std::endl;
    }

    for(typename T::iterator iter = in.begin()+2; iter != in.end(); ++iter) {
        if(*iter == P) continue;
        if(*iter == *(iter - 1)) continue; //duplicate or near- duplicate point; We don't want that mess.
        //std::cerr << "New point: " << *iter << "; angle=" << Tangent(P, *iter) << std::endl;
        //if(iter->y > 200) std::cerr << "==================\n";
        float product = CrossProduct(out[out.size()-2], out.back(), *iter);
        if (product < 0 || fabs(product) < EPS) {
            //the last three points are concave, remove points until they're not
            while((product < 0 || fabs(product) < EPS) && out.size() > 2) {
                //std::cerr << "concave: " << *(iter-2) << " " << *(iter-1) << " " << *iter << std::endl;
                //std::copy(out.begin(), out.end(), std::ostream_iterator<tCoord>(std::cerr, " "));
                //std::cerr << std::endl;
                out.pop_back();
                product = CrossProduct(out[out.size()-2], out.back(), *iter);
            }
        } else {
            //std::cerr << "Passed point: " << *iter << std::endl;
        }
        out.push_back(*iter);
        //std::copy(out.begin(), out.end(), std::ostream_iterator<tCoord>(std::cerr, " "));
        //std::cerr << std::endl;
    }
    float product = CrossProduct(out[out.size()-2], out.back(), P);
    while((product < 0 || fabs(product) < EPS) && out.size() > 2) {
        //std::cerr << "concave: " << *(iter-2) << " " << *(iter-1) << " " << *iter << std::endl;
        //std::copy(out.begin(), out.end(), std::ostream_iterator<tCoord>(std::cerr, " "));
        //std::cerr << std::endl;
        out.pop_back();
        product = CrossProduct(out[out.size()-2], out.back(), P);
    }
    //std::cerr << "=====\n";
    //for(typename T::iterator iter = out.begin(); iter != out.end(); ++iter) {
    //  std::cerr << *iter << std::endl;
    //}

}

Here is the call graph for this function:

Here is the caller graph for this function:

REAL tCoord::operator *

(

const tCoord &

a

)

const [inline]

returns a positive number if (a,*this) form a right-handed coordinate system, a negative number, if ... and 0, if a and *this are parallel.

Definition at line 112 of file tCoord.h.

References x, and y.

{return -x*a.y+y*a.x;}

tCoord tCoord::Turn

(

const tCoord &

a

)

const [inline]

complex multiplication: turns this by angle given in a

Definition at line 116 of file tCoord.h.

References tCoord(), x, and y.

Referenced by gJoystick::Act(), and Turn().

{return tCoord(x*a.x-y*a.y,y*a.x+x*a.y);}

Here is the call graph for this function:

Here is the caller graph for this function:

tCoord tCoord::Turn	(	REAL	x,
		REAL	y
	)			const [inline]

complex multiplication: turns this by angle given in x and y

Definition at line 118 of file tCoord.h.

References tCoord(), and Turn().

{return Turn(tCoord(x,y));}

Here is the call graph for this function:

tCoord tCoord::Conj

(

)

const [inline]

complex conjugation

Definition at line 120 of file tCoord.h.

References tCoord(), x, and y.

Referenced by gJoystick::Act().

{return tCoord(x,-y);}

Here is the call graph for this function:

Here is the caller graph for this function:

void tCoord::Print

(

std::ostream &

s

)

const

Prints the coordinate into a stream (format: "(x,y)").

Referenced by operator<<().

Here is the caller graph for this function:

void tCoord::Read

(

std::istream &

s

)

Reads the coordinate from a stream (format: "(x,y)").

Referenced by operator>>().

Here is the caller graph for this function:

---

Member Data Documentation

REAL tCoord::x

Definition at line 42 of file tCoord.h.

Referenced by gJoystick::ActInternal(), rFontContainer::BBox(), cWidget::Map::ClipperCircle::Begin(), cWidget::Map::ClipperRect::Begin(), cWidget::Map::ClipperCircle::Clip(), Conj(), CrossProduct(), display_cockpit_lucifer(), rGradient::DrawAt(), cWidget::Map::DrawMap(), cWidget::Map::DrawRimWalls(), F(), rGradient::GetGradientPt(), GrahamScan(), zShapePolygon::isInside(), NormSquared(), operator *(), operator *=(), operator+(), operator+=(), operator-(), operator-=(), operator=(), cWidget::WithCoordinates::Process(), cWidget::WithColorFunctions::ProcessGradient(), cWidget::Rectangle::Render(), cWidget::Map::Render(), cWidget::Label::Render(), rFontContainer::Render(), gCycle::Render2D(), cWidget::VerticalBarGauge::RenderCaption(), cWidget::BarGauge::RenderCaption(), cWidget::NeedleGauge::RenderGraph(), cWidget::VerticalBarGauge::RenderGraph(), cWidget::BarGauge::RenderGraph(), cWidget::BarGauge::RenderMinMax(), rGradient::SetGradientEdges(), rGradient::SetValues(), Tangent(), and Turn().

REAL tCoord::y

the stored coordinates

Definition at line 42 of file tCoord.h.

Referenced by gJoystick::ActInternal(), rFontContainer::BBox(), cWidget::Map::ClipperCircle::Begin(), cWidget::Map::ClipperRect::Begin(), cWidget::Map::ClipperCircle::Clip(), Conj(), CrossProduct(), display_cockpit_lucifer(), rGradient::DrawAt(), cWidget::Map::DrawMap(), cWidget::Map::DrawRimWalls(), F(), rGradient::GetGradientPt(), GrahamScan(), zShapePolygon::isInside(), NormSquared(), operator *(), operator *=(), operator+(), operator+=(), operator-(), operator-=(), operator=(), cWidget::WithCoordinates::Process(), cWidget::WithColorFunctions::ProcessGradient(), cWidget::Rectangle::Render(), cWidget::Map::Render(), cWidget::Label::Render(), rFontContainer::Render(), gCycle::Render2D(), cWidget::VerticalBarGauge::RenderCaption(), cWidget::BarGauge::RenderCaption(), cWidget::NeedleGauge::RenderGraph(), cWidget::VerticalBarGauge::RenderGraph(), cWidget::BarGauge::RenderGraph(), cWidget::BarGauge::RenderMinMax(), cWidget::WithCoordinates::SetFactor(), rGradient::SetGradientEdges(), rGradient::SetValues(), Tangent(), and Turn().

---

The documentation for this class was generated from the following file:

• src/tools/tCoord.h

---