tPolynomial< T > Class Template Reference

mathematical function (to be moved into tools sometime, and currently limited to linear functions) More...

#include <tPolynomial.h>

List of all members.

Public Member Functions
	tPolynomial ()
	constructor
	tPolynomial (int count)
	constructor
	tPolynomial (REAL newCoefs[], int count)
	constructor
	tPolynomial (REAL value)
	constructor for constant polynomial
	tPolynomial (tArray< REAL > newCoefs)
	constructor
	tPolynomial (const tPolynomial< T > &tf)
	constructor
	tPolynomial (std::string str)
	constructor
virtual	~tPolynomial ()
void	parse (std::string str)
virtual REAL	evaluate (REAL currentVarValue) const
	evaluates the function
REAL	operator() (REAL currentVarValue) const
	evaluation operator
tPolynomial< T > const	operator * (REAL constant) const
tPolynomial< T > const	operator * (const tPolynomial< T > &tfRight) const
tPolynomial< T > const	operator+ (REAL constant) const
tPolynomial< T > const	operator+ (const tPolynomial< T > &tfRight) const
tPolynomial< T > &	operator+= (const tPolynomial< T > &tfRight)
tPolynomial< T > const	substitute (const tPolynomial< T > &other) const
	Evaluate this(x) where x is another polynomial.
REAL &	operator[] (int index)
REAL const &	operator[] (int index) const
void	operator= (tPolynomial< T > const &other)
void	addConstant (REAL constant)
tPolynomial< T >	adaptToNewReferenceVarValue (REAL currentVarValue) const
tPolynomial< T >	translate (REAL currentVarValue) const
void	changeRate (REAL newRate, int newRateLength, REAL currentVarValue)
void	setRates (REAL newValues[], int newValuesLength, REAL currentVarValue)
void	setRates (tArray< REAL > newValues, REAL currentVarValue)
virtual T &	ReadSync (T &m)
virtual T &	WriteSync (T &m) const
virtual std::string	toString () const
tPolynomial< T > const	clamp (REAL min, REAL max, REAL currentVarValue)
int	Len () const
void	setAtSameReferenceVarValue (const tPolynomial< T > &other)
Protected Member Functions
void	setReferenceVarValue (REAL newReferenceVarValue)
void	growCoefsArray (int newLength)
Protected Attributes
REAL	referenceVarValue
	the evaluation is always done on (currentVarValue - referenceVarValue) rather than (currentVarValue)
tArray< REAL >	coefs
Friends
template<typename D>
bool	operator== (const tPolynomial< D > &left, const tPolynomial< D > &right)
template<typename D>
bool	operator!= (const tPolynomial< D > &left, const tPolynomial< D > &right)

---

Detailed Description

template<typename T>
class tPolynomial< T >

mathematical function (to be moved into tools sometime, and currently limited to linear functions)

Definition at line 45 of file tPolynomial.h.

---

Constructor & Destructor Documentation

template<typename T>

tPolynomial< T >::tPolynomial

(

)

[inline]

constructor

Definition at line 146 of file tPolynomial.h.

        : referenceVarValue(0.0),
        coefs(0)
{
    // Empty
}

template<typename T>

tPolynomial< T >::tPolynomial

(

int

count

)

[inline, explicit]

constructor

Parameters:

count

constructor

Definition at line 136 of file tPolynomial.h.

References tPolynomial< T >::coefs.

        : referenceVarValue(0.0),
        coefs(count)
{
    // Initialise to all 0's
    for (int i=0; i<coefs.Len(); i++)
        coefs[i] = 0.0f;
}

template<typename T>

tPolynomial< T >::tPolynomial	(	REAL	newCoefs[],
		int	count
	)			[inline]

constructor

Parameters:

count

constructor

Definition at line 154 of file tPolynomial.h.

References tPolynomial< T >::coefs.

        : referenceVarValue(0.0),
        coefs(count)
{
    for (int i=0; i<coefs.Len(); i++)
        coefs[i] = newCoefs[i];
}

template<typename T>

tPolynomial< T >::tPolynomial

(

REAL

value

)

[inline]

constructor for constant polynomial

Parameters:

value

constructor for constant polynomial

Definition at line 163 of file tPolynomial.h.

References tPolynomial< T >::coefs.

        : referenceVarValue(0.0),
        coefs(1)
{
    coefs[0] = value;
}

template<typename T>

tPolynomial< T >::tPolynomial

(

tArray< REAL >

newCoefs

)

[inline]

constructor

Parameters:

newCoefs

constructor

Definition at line 171 of file tPolynomial.h.

        : referenceVarValue(0.0),
        coefs(newCoefs)
{
    // Empty
}

template<typename T>

tPolynomial< T >::tPolynomial

(

const tPolynomial< T > &

tf

)

[inline]

constructor

Parameters:

tf	constructor

Definition at line 179 of file tPolynomial.h.

        : referenceVarValue(tf.referenceVarValue),
        coefs(tf.coefs)
{
    // Empty
}

template<typename T>

tPolynomial< T >::tPolynomial

(

std::string

str

)

[inline]

constructor

Definition at line 600 of file tPolynomial.h.

References tPolynomial< T >::parse().

  : referenceVarValue(0.0),
     coefs(0)
{
  parse(str);
}

Here is the call graph for this function:

template<typename T>

virtual tPolynomial< T >::~tPolynomial

(

)

[inline, virtual]

Definition at line 57 of file tPolynomial.h.

    {
    }

---

Member Function Documentation

template<typename T>

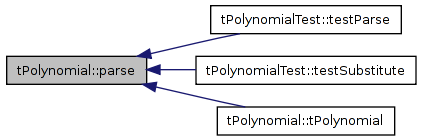
void tPolynomial< T >::parse

(

std::string

str

)

[inline]

Definition at line 608 of file tPolynomial.h.

References tPolynomial< T >::coefs, pos, REAL, and TPOLYNOMIAL_DELIMITER.

Referenced by tPolynomialTest::testParse(), tPolynomialTest::testSubstitute(), and tPolynomial< T >::tPolynomial().

{
    int pos;
    int prevPos = 0;
    int index = 0;

#define TPOLYNOMIAL_DELIMITER ';'

    pos = str.find(TPOLYNOMIAL_DELIMITER, 0);
    if(-1 != pos) {
      do{
        REAL value = atof(str.substr(prevPos, pos).c_str());
        coefs.SetLen(index + 2); // +1 because to write at index n, the len must be n+1. +1 to allocate a place for the element after the last ':'
        coefs[index] = value;
        
        prevPos = pos + 1;
        index ++;
      }
      while ( (pos = str.find(TPOLYNOMIAL_DELIMITER, prevPos)) != -1) ;

      coefs[index] = atof(str.substr(prevPos, pos).c_str());

    }
    else {
      coefs.SetLen(1);
      coefs[0] = atof(str.c_str());
    }
}

Here is the caller graph for this function:

template<typename T>

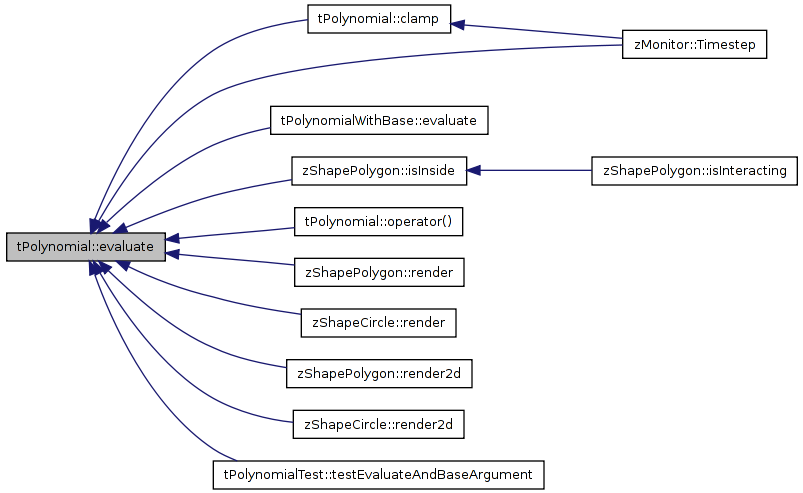
REAL tPolynomial< T >::evaluate

(

REAL

currentVarValue

)

const [inline, virtual]

evaluates the function

Definition at line 423 of file tPolynomial.h.

References tPolynomial< T >::coefs, REAL, and tPolynomial< T >::referenceVarValue.

Referenced by tPolynomial< T >::clamp(), tPolynomialWithBase< T >::evaluate(), zShapePolygon::isInside(), tPolynomial< T >::operator()(), zShapePolygon::render(), zShapeCircle::render(), zShapePolygon::render2d(), zShapeCircle::render2d(), tPolynomialTest::testEvaluateAndBaseArgument(), and zMonitor::Timestep().

{
    REAL deltaVariableValue = (currentVarValue - referenceVarValue);

    REAL res = 0.0;

    // Compute res = c[0] + c[1]*var + (c[2]/2)*var^2 + ... + (c[N]/N)*var^N
    for (int i=coefs.Len()-1; i>0; i--) {
        res = (res + coefs[i]/i) * deltaVariableValue;
    }
    if (coefs.Len()!=0)
        res += (coefs[0]);

    return res;

}

Here is the caller graph for this function:

template<typename T>

REAL tPolynomial< T >::operator()

(

REAL

currentVarValue

)

const [inline]

evaluation operator

Returns:

the function value

Definition at line 197 of file tPolynomial.h.

References tPolynomial< T >::evaluate().

{
    return evaluate( currentVarValue );
}

Here is the call graph for this function:

template<typename T>

tPolynomial< T > const tPolynomial< T >::operator *

(

REAL

constant

)

const [inline]

Definition at line 474 of file tPolynomial.h.

References tPolynomial< T >::coefs.

                                                                    {
    tPolynomial<T> tf(*this);

    for (int i=0; i<coefs.Len(); i++) {
        tf[i] *= constant;
    }
    return tf;
}

template<typename T>

tPolynomial< T > const tPolynomial< T >::operator *

(

const tPolynomial< T > &

tfRight

)

const [inline]

Definition at line 484 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::setAtSameReferenceVarValue().

                                                                                     {
    tPolynomial<T> tf;
    tf.setAtSameReferenceVarValue(tfRight);

    // If any Polygonial is of size 0, then the resulting one is too
    // Otherwise, it is the sum of both lenght, minus 1.
    int newLength =
        (0 == this->coefs.Len() || 0 == tfRight.coefs.Len())
        ? 0
        : (this->coefs.Len() + tfRight.coefs.Len() - 1);

    int oldLength = tf.coefs.Len();
    tf.coefs.SetLen(newLength);
    for (int i=oldLength; i<newLength; i++) {
        tf[i] = 0.0;
    }

    if (0 == newLength) {
        // Special case, nothing needs to be done
    }
    else {
        for (int i=0; i<this->coefs.Len(); i++) {
            for (int j=0; j<tfRight.coefs.Len(); j++) {
                tf[i+j] += (this->coefs[i]) * tfRight[j];
            }
        }
    }
    return tf;
}

Here is the call graph for this function:

template<typename T>

tPolynomial< T > const tPolynomial< T >::operator+

(

REAL

constant

)

const [inline]

Definition at line 515 of file tPolynomial.h.

                                                                    {
    tPolynomial<T> tf(*this);
    tf[0] += constant;
    return tf;
}

template<typename T>

tPolynomial< T > const tPolynomial< T >::operator+

(

const tPolynomial< T > &

tfRight

)

const [inline]

Definition at line 522 of file tPolynomial.h.

References tPolynomial< T >::adaptToNewReferenceVarValue(), tPolynomial< T >::coefs, and MAX.

                                                                                    {
    // Bring the polynomial to the same baseValue, so that the terms mean the same thing
    tPolynomial<T> tRebasedRight(tfRight.adaptToNewReferenceVarValue(this->referenceVarValue));

    int maxLength = MAX(this->coefs.Len(), tfRight.coefs.Len());

    // Set the lenght to the longest member of the addition
    tRebasedRight.coefs.SetLen(maxLength);

    for (int i=0; i<this->coefs.Len(); i++) {
        tRebasedRight[i] += coefs[i];
    }

    return tRebasedRight;
}

Here is the call graph for this function:

template<typename T>

tPolynomial< T > & tPolynomial< T >::operator+=

(

const tPolynomial< T > &

tfRight

)

[inline]

Definition at line 539 of file tPolynomial.h.

References tPolynomial< T >::adaptToNewReferenceVarValue(), tPolynomial< T >::coefs, and MAX.

                                                                           {
    // Bring the polynomial to the same baseValue, so that the terms mean the same thing
    tPolynomial<T> tRebasedRight = tfRight.adaptToNewReferenceVarValue(this->referenceVarValue);

    int maxLength = MAX(this->coefs.Len(), tfRight.coefs.Len());
    // Set the lenght to the longest member of the addition
    coefs.SetLen(maxLength);

    for (int i=0; i<maxLength; i++) {
        coefs[i] += tRebasedRight[i];
    }

    return *this;
}

Here is the call graph for this function:

template<typename T>

tPolynomial< T > const tPolynomial< T >::substitute

(

const tPolynomial< T > &

other

)

const [inline]

Evaluate this(x) where x is another polynomial.

Definition at line 558 of file tPolynomial.h.

References tPolynomial< T >::setAtSameReferenceVarValue().

Referenced by tPolynomialTest::testSubstitute().

                                                                                   {
  tPolynomial<T> tf(0);
  tf.setAtSameReferenceVarValue(other);
  for(int i=this->Len()-1; i>0; i--) {
    tf = (tf + (*this)[i]) * other;
  }
  if(0 != this->Len()) {
    tf = tf + (*this)[0];
  }

  return tf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename T>

REAL & tPolynomial< T >::operator[]

(

int

index

)

[inline]

Definition at line 572 of file tPolynomial.h.

References tPolynomial< T >::coefs.

{
    // Manually growing the array to set all new elements to 0
    if (index >= coefs.Len()) {
        int previousLength = coefs.Len();
        coefs.SetLen(index + 1);
        for (int i=previousLength; i<coefs.Len(); i++) {
            coefs[i] = 0.0;
        }
    }

    return coefs[index];
}

template<typename T>

REAL const & tPolynomial< T >::operator[]

(

int

index

)

const [inline]

Definition at line 587 of file tPolynomial.h.

References tPolynomial< T >::coefs.

{
    return coefs[index];
}

template<typename T>

void tPolynomial< T >::operator=

(

tPolynomial< T > const &

other

)

[inline]

Definition at line 593 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::referenceVarValue.

{
    coefs = other.coefs;
    referenceVarValue = other.referenceVarValue;
}

template<typename T>

void tPolynomial< T >::addConstant

(

REAL

constant

)

[inline]

Definition at line 78 of file tPolynomial.h.

                                    {
        if (coefs.Len()==0) {
            coefs.SetLen(1);
            coefs[0] = 0;
        } 
        coefs[0] += constant;
    }

template<typename T>

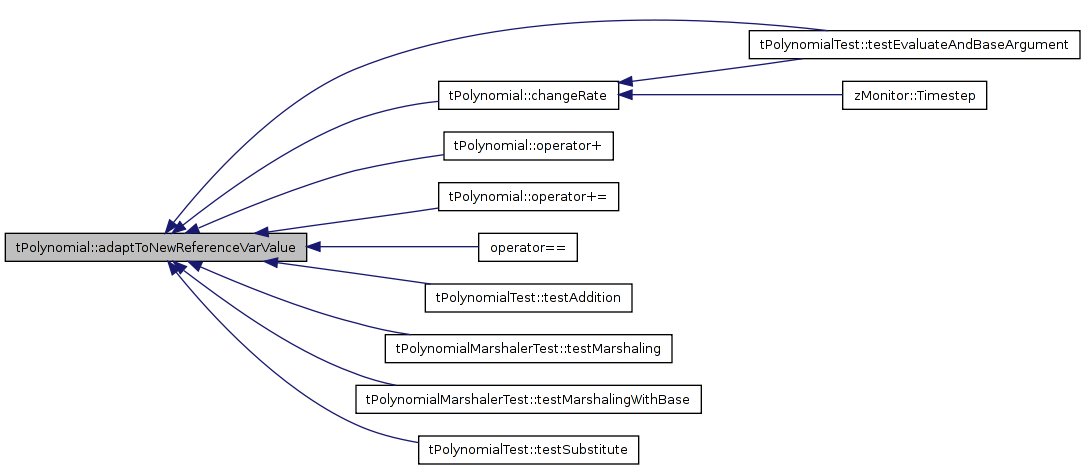
tPolynomial< T > tPolynomial< T >::adaptToNewReferenceVarValue

(

REAL

currentVarValue

)

const [inline]

Definition at line 309 of file tPolynomial.h.

References tPolynomial< T >::coefs, REAL, tPolynomial< T >::referenceVarValue, and tPolynomial< T >::setReferenceVarValue().

Referenced by tPolynomial< T >::changeRate(), tPolynomial< T >::operator+(), tPolynomial< T >::operator+=(), operator==(), tPolynomialTest::testAddition(), tPolynomialTest::testEvaluateAndBaseArgument(), tPolynomialMarshalerTest::testMarshaling(), tPolynomialMarshalerTest::testMarshalingWithBase(), and tPolynomialTest::testSubstitute().

{
    tPolynomial<T> tf(*this);

    // Compute the coefficients at "currentVarValue" (var for short)
    // c0' = c0 + (c1/sum(1))*var + (c2/sum(2))*var^2 + ... + (c[N]/sum(N))*var^N
    // c1' = c1 + (c2/sum(1))*var + ... + (c[N]/sum(N-1))*var^(N-1)
    // c2' = c2 + ... + (c[N]/sum(N-2))*var^(N-2)
    // ...
    // c[N-1] = c[N-1] + (c[N]/sum(1))*var
    // c[N] = c[N]
    //
    // so:
    // [0   , 0 , a] at currentVarValue=0 will become
    // [9a/2, 3a, a] at currentVarValue=3

    REAL deltaVariableValue = currentVarValue - referenceVarValue;

    // Compute for each coefficient their new value
    for (int coefIndex=0; coefIndex<coefs.Len(); coefIndex++) {
        REAL newCoefValue = 0.0;
        for (int j=coefs.Len()-1; j>coefIndex; j--) {
            newCoefValue = (newCoefValue + coefs[j] ) * deltaVariableValue /(j - coefIndex);
        }
        tf.coefs[coefIndex] += newCoefValue;
    }

    tf.setReferenceVarValue(currentVarValue);
    return tf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename T>

tPolynomial< T > tPolynomial< T >::translate

(

REAL

currentVarValue

)

const [inline]

Definition at line 344 of file tPolynomial.h.

References tPolynomial< T >::coefs, REAL, tPolynomial< T >::referenceVarValue, and tPolynomial< T >::setReferenceVarValue().

Referenced by tPolynomialTest::testTranslate().

{
    tPolynomial<T> tf(*this);

    // Compute the coefficients at "currentVarValue" (var for short)
    // c0' = c0 + (c1)*var + (c2)*var^2 + ... + (c[N])*var^N
    // c1' = c1 + (c2)*var + ... + (c[N])*var^(N-1)
    // c2' = c2 + ... + (c[N])*var^(N-2)
    // ...
    // c[N-1] = c[N-1] + (c[N])*var
    // c[N] = c[N]
    //
    // so:
    // [0   , 0 , a] at currentVarValue=0 will become
    // [9a, 6a, a] at currentVarValue=3

    REAL deltaVariableValue = currentVarValue - referenceVarValue;

    // Compute for each coefficient their new value
    for (int coefIndex=0; coefIndex<coefs.Len(); coefIndex++) {
        REAL newCoefValue = 0.0;
        for (int j=coefs.Len()-1; j>coefIndex; j--) {
            newCoefValue = (newCoefValue + coefs[j] ) * deltaVariableValue;
        }
        tf.coefs[coefIndex] += newCoefValue;
    }

    tf.setReferenceVarValue(currentVarValue);
    return tf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename T>

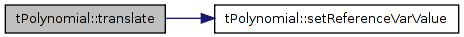
void tPolynomial< T >::changeRate	(	REAL	newRate,
		int	newRateLength,
		REAL	currentVarValue
	)			[inline]

Definition at line 379 of file tPolynomial.h.

References tPolynomial< T >::adaptToNewReferenceVarValue(), and tPolynomial< T >::coefs.

Referenced by tPolynomialTest::testEvaluateAndBaseArgument(), and zMonitor::Timestep().

{
    if (coefs.Len() <= newRateIndex) {
        int oldLength = coefs.Len();
        coefs.SetLen(newRateIndex + 1);
        for (int i=oldLength; i<newRateIndex; i++) {
            coefs[i] = 0.0;
        }
    }

    *this = adaptToNewReferenceVarValue(currentVarValue);

    coefs[newRateIndex] = newRate;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename T>

void tPolynomial< T >::setRates	(	REAL	newValues[],
		int	newValuesLength,
		REAL	currentVarValue
	)			[inline]

This perform a hard setting of all the coefficients

Definition at line 398 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::setReferenceVarValue().

{
    if (coefs.Len() < newValuesLength) {
        int oldLength = coefs.Len();
        coefs.SetLen(newValuesLength + 1);
        for (int i=oldLength; i<newValuesLength; i++) {
            coefs[i] = 0.0;
        }
    }

    setReferenceVarValue(currentVarValue);

    for (int i=0; i<newValuesLength; i++) {
        coefs[i] = newValues[i];
    }
}

Here is the call graph for this function:

template<typename T>

void tPolynomial< T >::setRates	(	tArray< REAL >	newValues,
		REAL	currentVarValue
	)			[inline]

Definition at line 416 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::setReferenceVarValue().

{
    coefs = newValues;
    setReferenceVarValue(currentVarValue);
}

Here is the call graph for this function:

template<typename T>

T & tPolynomial< T >::ReadSync

(

T &

m

)

[inline, virtual]

Definition at line 456 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::referenceVarValue.

Referenced by operator>>(), and tPolynomialWithBase< T >::ReadSync().

{
    m >> referenceVarValue;

    // Read the length
    int newLength = 0;
    m >> newLength;
    coefs.SetLen(newLength);

    for (int i=0; i<coefs.Len(); i++)
    {
        m >> coefs[i];
    }

    return m;
}

Here is the caller graph for this function:

template<typename T>

T & tPolynomial< T >::WriteSync

(

T &

m

)

const [inline, virtual]

Definition at line 441 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::referenceVarValue.

Referenced by tPolynomialWithBase< T >::WriteSync().

{
    m << referenceVarValue;
    // write length
    m << coefs.Len();

    for (int i=0; i<coefs.Len(); i++)
    {
        m << coefs[i];
    }

    return m;
}

Here is the caller graph for this function:

template<typename T>

std::string tPolynomial< T >::toString

(

)

const [inline, virtual]

Definition at line 638 of file tPolynomial.h.

References tPolynomial< T >::coefs, and tPolynomial< T >::referenceVarValue.

Referenced by tPolynomialMarshalerTest::testMarshaling(), tPolynomialTest::testSubstitute(), and tPolynomialTest::testTranslate().

                                         {
    std::ostringstream ostr("");

    ostr << "base :" << referenceVarValue << " lenght:" << coefs.Len();

    for (int i=0; i<coefs.Len(); i++) {
        ostr << " c[" << i << "]:" << coefs[i];
    }
    return ostr.str();
}

Here is the caller graph for this function:

template<typename T>

tPolynomial< T > const tPolynomial< T >::clamp	(	REAL	minValue,
		REAL	maxValue,
		REAL	currentVarValue
	)			[inline]

If the current polynomial is within the range, return a copy of itself Otherwise, return a new polynomial that is bound by the range

Definition at line 655 of file tPolynomial.h.

References tPolynomial< T >::coefs, tPolynomial< T >::evaluate(), and REAL.

Referenced by zMonitor::Timestep().

{
    tPolynomial<T> tf(*this);

    REAL valueAt = evaluate(currentVarValue);
    if (valueAt < minValue) {
        tf[0] = minValue;
        for (int i=1; i<coefs.Len(); i++) {
            if (tf[i] < 0) {
                tf[i] = 0.0;
            }
        }
    }
    if (maxValue < valueAt) {
        tf[0] = maxValue;
        for (int i=1; i<coefs.Len(); i++) {
            if (tf[i] > 0) {
                tf[i] = 0.0;
            }
        }
    }

    return tf;
}

Here is the call graph for this function:

Here is the caller graph for this function:

template<typename T>

int tPolynomial< T >::Len

(

)

const [inline]

Definition at line 104 of file tPolynomial.h.

Referenced by zMonitor::Timestep().

                   {
        return coefs.Len();
    };

Here is the caller graph for this function:

template<typename T>

void tPolynomial< T >::setAtSameReferenceVarValue

(

const tPolynomial< T > &

other

)

[inline]

Will change our referenceVarValue to that of the designated object.

Definition at line 684 of file tPolynomial.h.

References a, REAL, and tPolynomial< T >::referenceVarValue.

Referenced by tPolynomialMarshaler< T >::marshal(), tPolynomial< T >::operator *(), and tPolynomial< T >::substitute().

{
  REAL a = other.referenceVarValue;
  referenceVarValue = a;
  //  referenceVarValue = other.referenceVarValue;
}

Here is the caller graph for this function:

template<typename T>

void tPolynomial< T >::setReferenceVarValue

(

REAL

newReferenceVarValue

)

[inline, protected]

Definition at line 110 of file tPolynomial.h.

Referenced by tPolynomial< T >::adaptToNewReferenceVarValue(), tPolynomial< T >::setRates(), and tPolynomial< T >::translate().

                                                         {
        referenceVarValue = newReferenceVarValue;
    }

Here is the caller graph for this function:

template<typename T>

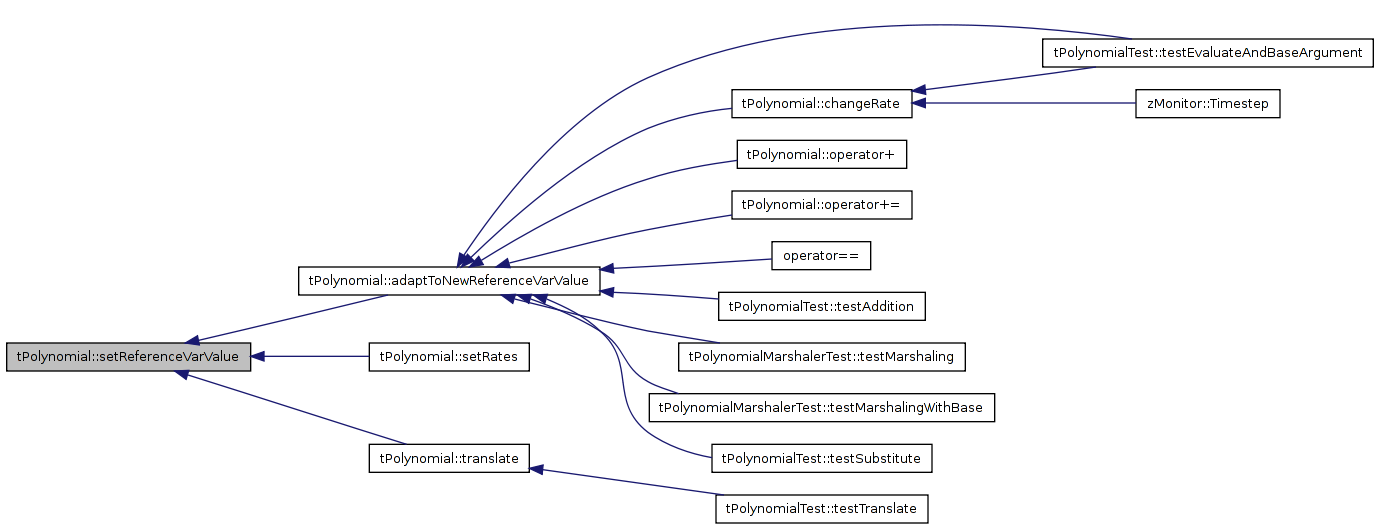
void tPolynomial< T >::growCoefsArray

(

int

newLength

)

[protected]

---

Friends And Related Function Documentation

template<typename T>

template<typename D>

bool operator==	(	const tPolynomial< D > &	left,
		const tPolynomial< D > &	right
	)			[friend]

template<typename T>

template<typename D>

bool operator!=	(	const tPolynomial< D > &	left,
		const tPolynomial< D > &	right
	)			[friend]

---

Member Data Documentation

template<typename T>

REAL tPolynomial< T >::referenceVarValue [protected]

the evaluation is always done on (currentVarValue - referenceVarValue) rather than (currentVarValue)

Definition at line 116 of file tPolynomial.h.

Referenced by tPolynomial< T >::adaptToNewReferenceVarValue(), tPolynomial< T >::evaluate(), tPolynomial< T >::operator=(), operator==(), tPolynomial< T >::ReadSync(), tPolynomial< T >::setAtSameReferenceVarValue(), tPolynomial< nMessage >::setReferenceVarValue(), tPolynomial< T >::toString(), tPolynomial< T >::translate(), and tPolynomial< T >::WriteSync().

template<typename T>

tArray<REAL> tPolynomial< T >::coefs [protected]

Definition at line 117 of file tPolynomial.h.

Referenced by tPolynomial< T >::adaptToNewReferenceVarValue(), tPolynomial< nMessage >::addConstant(), tPolynomial< T >::changeRate(), tPolynomial< T >::clamp(), tPolynomial< T >::evaluate(), tPolynomial< nMessage >::Len(), tPolynomial< T >::operator *(), tPolynomial< T >::operator+(), tPolynomial< T >::operator+=(), tPolynomial< T >::operator=(), operator==(), tPolynomial< T >::operator[](), tPolynomial< T >::parse(), tPolynomial< T >::ReadSync(), tPolynomial< T >::setRates(), tPolynomial< T >::toString(), tPolynomial< T >::tPolynomial(), tPolynomial< T >::translate(), and tPolynomial< T >::WriteSync().

---

The documentation for this class was generated from the following file:

• src/tools/tPolynomial.h

---